Phase Change Materials

Recent years have seen a surge in interest to rationalize the energy consumption motivated by the need of minimizing environmental effects and its cost to the world economy. The achievement of these ambitious goals requires efficient energy storage technologies to reduce wastes and buffer the period between energy production and consumption. Among other technologies, the named Phase Change Materials (PCM) offer an excellent low-cost option to help for this purpose.

The high latent heat of the solid/liquid phase change characteristic of these materials allows very high energy storage densities within a narrow temperature range. This high energy density allows less weight and volume, making those materials ideal in applications ranging from power plants to micro-electronic thermal management, passing for Smart textile, air conditioning in buildings, waste heat recovery, combination with construction materials to increase the thermal energy storage capacity of construction elements in light structures, etc.

Our research focuses on model development and realistic simulations of these materials. In particular, the appropriate modeling and efficient computation of the convective motions within the liquid phase are challenging but key to designing successful technologies based on PCMs We investigate how to improve this modeling in different scenarios, like in microgravity, nano-enhanced PCMs, high Rayleigh number regimes, etc.

Phase Change Materials in aerospace applications

The usual cycles of operation of devices onboard spacecrafts suit well with the heat storage and discharge cycles of PCMs. Thus, thermal control using PCMs in microgravity is widely used in space systems (Mars Rover, ESA launcher VEGA,etc), for low and high temperature applications, to avoid temperature peaks coming from electronic devices, power electrical components, control battery temperature in lunar and Mars rovers, or even to refrigerate food and biological waste samples in manned spacecrafts.

Furthermore, PCMs involve technology with high potential in many proposed future missions that require very tight and stable temperature (±1°C), deep cryogenic temperatures, high flux acquisition (> 100W/cm^2) and minimization of mass and power use.

Nowadays, hundredths of natural and synthetic PCMs are known at a broad range of operating temperatures. However, a significant issue in thermal regulation with these materials is their low conductivity, specially in paraffins at room temperatures. This leads to very long times during the heat storage and discharge phases and reduces their usability and performance on heat control.

On ground applications, the main choice to reduce the problem a of low conductivity is to promote convective motions within the liquid phase of the PCM. Convective motions driven by gradients of density induced by differences of temperature can enhance the heat transfer rate about an order of magnitude respect to conductive heat transfer. However, this strategy is not applicable in microgravity. Another approach to accelerate the heat transfer is to place a large area of PCM in contact with high conductivity materials such as metallic fins or metallic foams. Whereas this solution is applicable as well under microgravity conditions, it increases the mass and size of the devices, and convective driving is reduced or even suppressed.

A mechanism to enhance the heat transfer on PCMs in microgravity, without increasing mass and volume, is to benefit from the Marangoni flow induced by thermal gradients of surface tension. We have studied the influence of thermocapillarity on PCM melting both computationally and in parabolic flight experiments. This requires selecting a PCM with a phase change temperature complying with design limits, high latent heat and the best possible thermal conductivity in liquid and solid phases. We have studied the melting dynamic of n-octadecane, which exhibits a solid/liquid phase change within the temperature range of spacecraft payloads and exhibits stability and no undercooling.

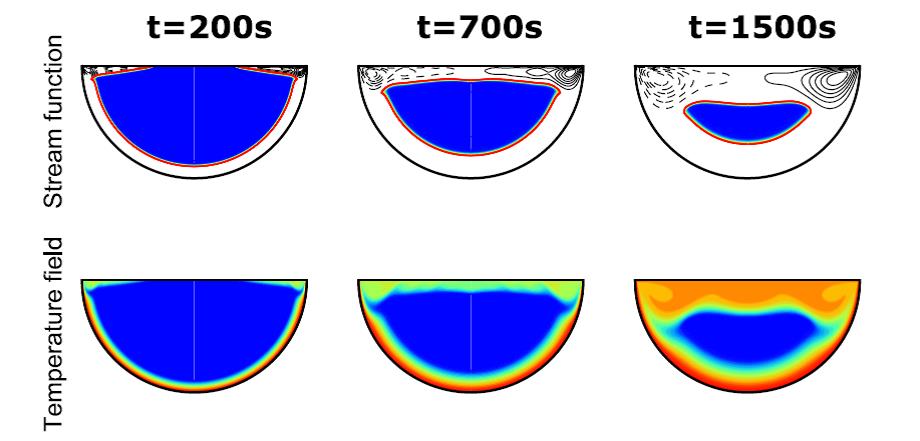
We find that thermocapillarity acting on free surfaces of PCMs in microgravity have a powerful influence on the heat transfer rate, decreasing the total melting time to about one third to one fourth for geometries typical of encapsulated materials of radius 2 cm respect to melting driven only by conductive transport. This strong enhancement of heat transfers indicates that thermocapillarity can be used on spacecrafts applications where quick heat exchangers are required to extract large amounts of heat without increasing the payload

• Heat transfer performance and melting dynamic of a phase change material subjected to thermocapillary effects.
  S. Madruga and C. Mendoza.
  International Journal of Heat and Mass Transfer. 109, 501-510 (2017). doi: 10.1016/j.ijheatmasstransfer.2017.02.025 ; paper.pdf
• Enhancement of heat transfer rate on phase change materials with thermocapillary flows.
  S. Madruga and C. Mendoza.
  European Physical Journal Special Topics. 226, 1169-1176 (2017). doi: 10.1140/epjst/e2016-60207-7 ; paper.pdf

Nano-enchanced Phase Change Materials

A major issue in thermal regulation with PCMs is the low conductivity typical of these materials, which leads to long times during the heat storage and release phases. Many solutions have been proposed to remedy this shortcoming by introducing high conductivity metals within the PCM, often as metallic fins, or embedding the PCM in a metallic porous foam. An innovative and promising solution which holds high potential to increase the heat transfer rate, without adding complexity to the device, is the dispersión in the PCM of metallic particles of sizes in the range of tens of nanometers at small volume fractions, forming the named Nan-oenhanced PCM (NePCM). In contrast to micrometer size particles, they do not sediment, clog or produce considerable pressure drops. The potential of metallic nanoparticles in heat transfer applications with PCMs has prompted the study of these systems during most of the last decade

The overall interplay between conduction, where metallic nanoparticles always speed up the heat transfer, and convection, where viscosity and conductivity are competitive, determine the final heat transfer performance of nano-enhanced PCMs. Simulations of nanoparticle enhanced PCMs have been carried out mostly using versions of phase field models, like the Maxwell-Garnett model for conductivity and Brinkmann for viscosity. However, these models tend to underestimate the value of these transport coefficients as a function of nanoparticle concentrations and are not completely satisfactory.

A different approach to determine the effective transport coefficients is to use fits to available experimental data. While due to the complexity of base fluid and nanoparticles interactions no current theories or single correlations can predict the broad spectrum of experimental data, predictions from some empirical fits (like Corcione's) are better than proposed theoretical models at a wide range of volume fractions of nanoparticles.

We have studied the melting of a paraffin wax with dispersed Al₂ O₃ nanoparticles, following two models to calculate the transport coefficients: (i) the mean field models due to Maxwell-Garnett for conductivity and Brinkmann for viscosity, (ii) an empirical fit to experimental data due to Corcione. We have shown that the usual mean field models used in nano-enhanced PCM literature underestimate the duration of the melting process compared to empirical models based on experimental data in most of the parameter space. These results agree with experiments carried out by Ho and Gao in n-octadecane with dispersed Al₂ O₃ nanoparticles, where no improvement of the heat transfer rate in the convective regime was observed. 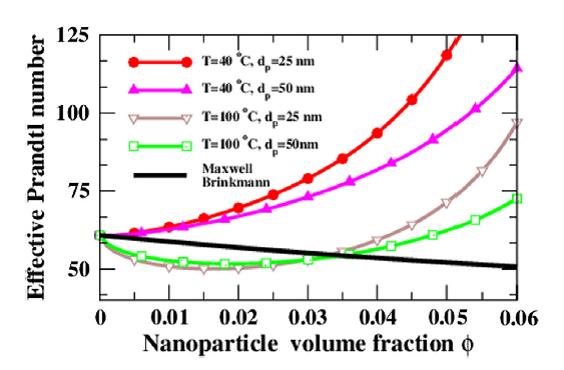We show how the effective Prandtl number can be used to estimate the heat transfer performance of nanoparticle/liquified PCM combinations.

We find that nanoparticles of small size, high temperature, and small volume fractions favor a lower effective Prandtl number -and enhanced rate of melting- for the empirical models and the opposite situation promotes a lower effective Prandtl number for mean field models. The most frequent cases studied numerically in the literature are found within the favorable regime of mean field models, which leads to an overestimation of the reduction of melting times for the convective regime compared with the empirical models. However, we have shown that is possible to choose the size of alumina nanoparticles, volume fractions, and temperatures where the NePCM exhibits an improved heat transfer rate respect to what is predicted by the mean field models. In these situations, NePCM become even more attractive for thermal management and energy storage applications. Thes results

Melting dynamics of a phase change material (PCM) with dispersed metallic nanoparticles using transport coefficients from empirical and mean field models.
S. Madruga and G.S. Mischlich.
Applied Thermal Engineering. 124, 1123-1133 (2017). doi: doi:10.1016/j.applthermaleng.2017.06.097; paper.pdf

Coarsening and scaling laws in vertical melting

The Rayleigh-Bénard problem of a liquid layer heated from below is characterized by three physical magnitudes: the difference of temperature between the plates, the heat flux, and the type of fluid. These provide three dimensionless numbers: Rayleigh Ra, Nusselt Nu, and Prandtl Pr; respectively, which characterize the solutions of this problem.

At the regime of high numbers, the relation between Rayleigh and Nussselt numbers Nu(Ra; Pr) has been thoroughly studied and found that mostly matches a power law Nu ~ Ra ^α. The exponent alpha generally is within a range between 1/4 and 1/3, and the numerical results show a dependence of the exponent with Ra.

We have studied this scaling in the presence of phase change with a moving and deformable solid/liquid interface. The presence of phase change introduces an additional number related to the source of latent heat, the Stefan number, that complicates the problem. In spite of that, we find that the averaged value of the numeric exponent 0.29 is consistent with experimental results on moderately high Rayleigh numbers Ra, and theoretical models predicting 2/7 on high Rayleigh number convection.

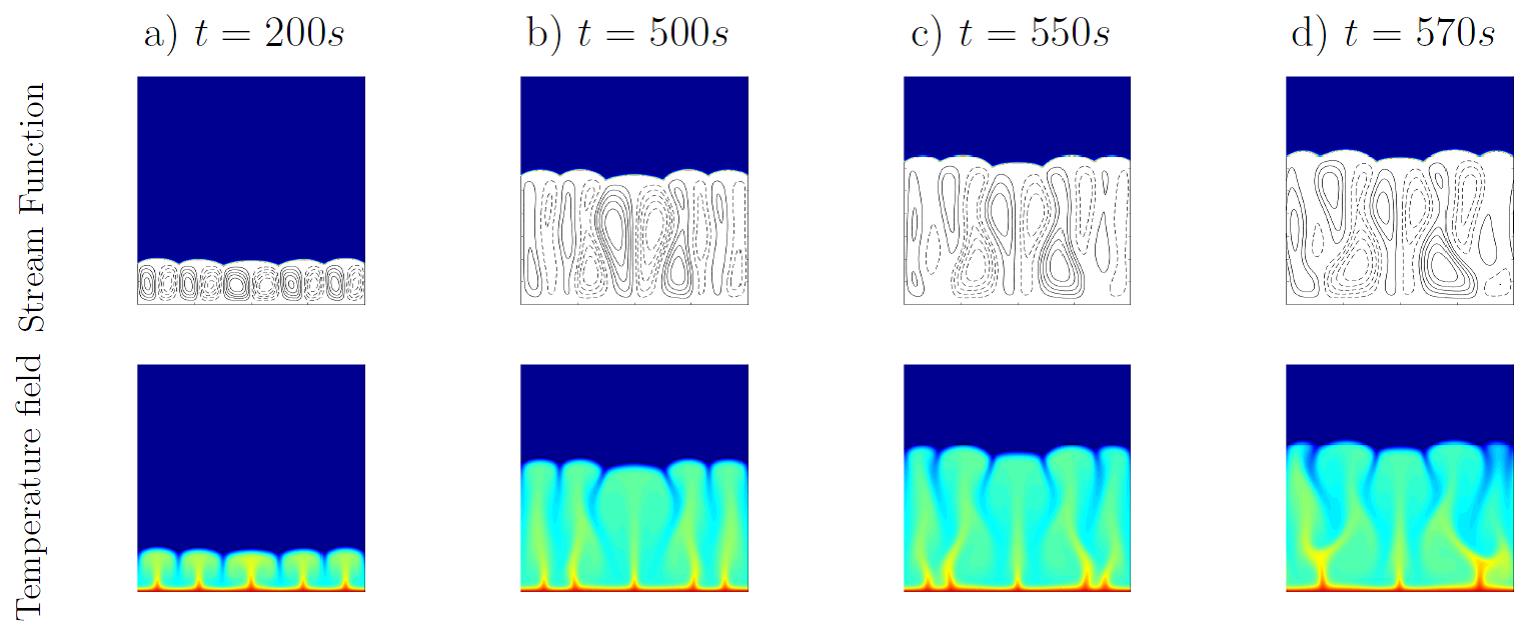
The most appealing feature of vertical melting is that we scan a very wide range of Rayleigh numbers for the liquid phase of the PCM, from characteristic values of conductive transport to values associated with turbulence, without changing any external parameter of the problem. We find that turbulence takes place after plume coarsening, or even after a coarsening cascade in some cases.

We observe that most of the representations of the melting process are ruled by power laws, although not all of them. Thus the number of plumes, some regimes of the Rayleigh number as a function of time, the number of plumes after the primary and secondary instability, the onset of the first and second instabilities, the thermal and kinetic boundary layers at the turbulent regime follow simple power laws. Other turbulent exponents, like the scaling of the thermal and kinematic boundary layers, δ_T ~ Ra^0.29, and δ_u ~ Ra^0.16 respectively, do not fit well with the predictions of the Blasius-Prandtl scaling. However, we notice that this disagreement appears as well in other numerical and experimental works that report similar values to this work.

• Dynamic of plumes and scaling during the melting of a Phase Change Material heated from below.
  S. Madruga and J. Curbelo
  Under review. arXiv: arxiv.org/submit/2078194 ; paper.pdf
• Experimental and numerical study of melting of the phase change material tetracosane.
  S. Madruga, A. Haruki, A. Horibe.
  In preparation.

Micro-energy harvesters

Wireless sensors are employed in a wide range of applications to monitor environmental variables, industrial process, health parameters, etc. Batteries usually power them. However in applications involving remote locations, extreme conditions or the need of truly autonomous systems the requirement of periodic replacement or recharging of batteries makes them impractical.

Among the different technologies aimed at power low consume sensors - as solar cells, piezoelectric devices, electrostatic methods, etc.- thermoelectric energy harvesting looks one of the b est solutions to create autonomous monitoring sensors. Thermoelectric generators transform temperature gradients across them into electrical energy by means of the Seebeck effect.

Frequently, thermoelectric energy harvesters require a substantial temperature difference along the device structure. This has restricted its use to applications where a hot metal surface is available. An alternative approach is to take advantage of ambient temperature variations using a heat storage unit, which is filled with a PCM to create a sustained temperature gradient in time.

We are investigating how to couple the thermoelectric generators with PCMs to design micro-energy harvesters that optimize the electric energy output to the wireless sensors. In particular, we are interested in the design of autonomous micro-harvesters to power structural health-monitoring systems in aircrafts, like humidity, temperature, and acoustic-ultrasonic parameters. Removing wires and creating robust autonomous micro-harversters decreases the complexity, weight of aircrafts and increase their security by the augmented monitoring options.